手动计算渐变
以下代码应该是相当不言自明的,除了几个新元素:
random_uniform()函数在图形中创建一个节点,它将生成包含随机值的张量,给定其形状和值作用域,就像 NumPy 的rand()函数一样。assign()函数创建一个为变量分配新值的节点。 在这种情况下,它实现了批次梯度下降步骤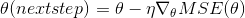 。
。- 主循环一次又一次(共
n_epochs次)执行训练步骤,每 100 次迭代都打印出当前均方误差(MSE)。 你应该看到 MSE 在每次迭代中都会下降。
housing = fetch_california_housing()m, n = housing.data.shapem, n = housing.data.shape# np.c_按colunm来组合arrayhousing_data_plus_bias = np.c_[np.ones((m, 1)), housing.data]scaled_housing_data_plus_bias = scale(housing_data_plus_bias)n_epochs = 1000learning_rate = 0.01X = tf.constant(scaled_housing_data_plus_bias, dtype=tf.float32, name="X")y = tf.constant(housing.target.reshape(-1, 1), dtype=tf.float32, name="y")theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0), name="theta")y_pred = tf.matmul(X, theta, name="predictions")error = y_pred - ymse = tf.reduce_mean(tf.square(error), name="mse")gradients = 2/m * tf.matmul(tf.transpose(X), error)training_op = tf.assign(theta, theta - learning_rate * gradients)init = tf.global_variables_initializer()with tf.Session() as sess:sess.run(init)for epoch in range(n_epochs):if epoch % 100 == 0:print("Epoch", epoch, "MSE =", mse.eval())sess.run(training_op)best_theta = theta.eval()
