1. 数据结构的基本概念

“数据结构”是研究各种数据的特性以及数据之间存在的关系，进而根据实际应用的要求，合理地组织和存储数据，设计出相应的算法。

数据是对客观事物的符号表示，

• 数据元素（节点）：数据的基本单位，在程序中通常作为一个整体进行考虑和处理。一个数据元素可以由若干个数据项组成。
• 数据项：具有独立含义的最小标识单位。例如，一条数据记录可以称为一个数据元素，数据记录的某个字段就是一个数据项。
• 数据结构：相互之间存在一种或多种特点关系的数据元素的集合。

1.1. 数据的逻辑结构

数据的逻辑结构：数据元素与数据元素之间的逻辑关系。可以分为四类基本结构：

• 集合：结构中的数据元素属于一个集合（集合类型元素之间过于松散）
• 线性结构：结构中的数据元素存在一对一的关系
• 树形结构：结构中的数据元素存在一对多的关系
• 图形结构：结构中的数据元素存在多对多的关系

数据的逻辑结构可以用以下的二元组来表示：

S=(D,R)

其中，D是数据节点的有限集合，R是D上的关系的有限集合，其中每个关系都是从D到D的关系。

例如：

S = (D,R)
D = {1,2,3,4}
R = {r}
r = {<1,2>,<1,3>,<3,4>}

说明：

• 尖括号表示有向关系，例如<a,b>，表示a→b
• 圆括号表示无向关系，例如(a,b)，表示a→b,b→a
• 前驱结点：中a是b的前驱结点
• 后继结点：中b是a的后继结点
• 开始结点：没有前驱结点
• 终端结点：没有后继结点
• 内部结点：既有前驱结点，又有后继结点

1.2. 数据的存储结构

数据在计算机中的存储表示称为数据的存储结构，又称物理结构。
数据存储到计算机中即要求存储各节点的数值，又要存储结点与结点之间的逻辑关系。
以下介绍四种基本的存储结构：顺序存储、链式存储、索引存储、散列存储。

1、顺序存储结构

顺序存储结构是把逻辑上相邻的元素存储在一组连续的存储单元中，其元素之间的逻辑关系由存储单元地址间的关系隐含表示。

优点：节省存储空间，只需要存储数据结点，并不需要存储结点的逻辑关系。
缺点：不便于修改，插入和删除某个结点需要修改一系列的结点。

2、链式存储结构

链式存储结构，给每个结点增加指针字段，用于存放临近结点的存储地址，每个结点占用两个连续的存储单元，一个存放数据，一个存放临近结点（前驱/后继结点）的地址。

优点：便于修改，修改时只需要修改结点的指针字段，不需要移动其他结点。
缺点：占用存储空间，因为需要存储结点之间的逻辑关系。因为结点之间不一定相邻，因此不能对结点进行随机访问。

3、索引存储结构

索引存储结构即在存储结点的同时，增加索引表，索引表的索引项为：（关键字，地址），关键字标识结点，地址为结点的指针。各结点的地址在索引表中是依次排列的。

优点：可以快速查找，可以随机访问，方便修改。
缺点：建立索引表增加了时间和空间的开销。

4、散列存储结构

散列存储结构是根据结点的值确定结点的存储地址。以结点作为自变量，通过散列函数算出结果i，再把i作为结点的存储地址。

优点：查找速度快，适用于快速查找和插入的场景。
缺点：只存结点数据，不存结点之间的关系。

1.3. 数据的运算

数据的运算就是施加于数据的操作，例如对一张表进行增删改查操作，一般数据结构中的运算除了加减乘除外还会涉及算法问题。

1.4. 数据结构与数据类型

按某种逻辑关系组成的数据元素，按一定的存储方式存储于计算机中，并在其上定义了一个运算的集合，称为一个数据结构。

数据结构 = 数据的逻辑结构 + 数据的存储结构 + 数据的运算(算法)

数据类型是程序设计语言中对数据结构的实现，数据类型明显或隐含地规定了数据的取值范围、存储方式及允许进行的运算。

常用的数据类型：

1. 基本数据类型
2. 指针类型
3. 数组类型
4. 结构体类型
5. 组合体类型
6. 自定义类型

2. 算法的基本概念

2.1. 算法及其特征

算法是对特定问题求解步骤的描述，是指令的有限序列，每条指令包含一个或多个操作。

特点：

• 有穷性：有限的步骤和有限的时间内完成
• 确定性：每个指令有确定的含义
• 可行性：算法是可以实现的
• 输入性：一个或多个输入
• 输出性：一个或多个输出

2.2. 算法描述

1. 输入语句
2. 输出语句
3. 赋值语句
4. 条件语句
5. 循环语句
6. 返回语句（return）
7. 定义函数语句
8. 调用函数语句

2.3. 算法分析

2.3.1. 时间复杂度

算法分析主要涉及时间复杂度和空间复杂度。一般情况我们讨论时间复杂度。

• 频度：某语句在算法中被执行的次数。
• T(n)：所有语句的频度之和，n为问题规模。
• 时间复杂度：当n趋于无穷大时，T(n)的数量级。记作T(n)=O(f(n)), O的含义是T(n)的数量级。

用数量级O(f(n))表示算法执行时间T(n)时，f(n)一般去简单形式：1, log_2n, n, nlog_2n, n^2, n^3, 2^n。

时间复杂度的关系如下：

O(1) < O(log_2n) < O(n) < O(nlog_2n) < O(n^2) < O(n^3) < O(2^n)

时间复杂度函数对比（图片来自网络）:

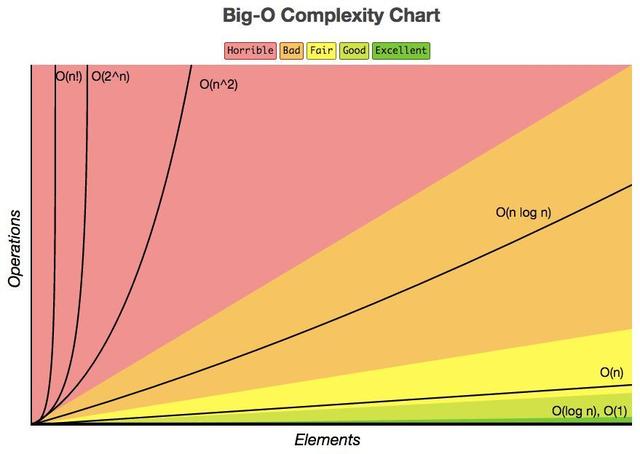
2.3.2. 空间复杂度

一个算法的空间复杂度是指该算法所耗费的存储空间，计算公式计作：S(n) = O(f(n))。其中 n 也为数据的规模，f(n) 在这里指的是 n 所占存储空间的函数。

常用的空间复杂度：

• 空间复杂度 O(1)
• 空间复杂度 O(n)
• 空间复杂度 O(n^2)

文章参考：

《数据结构教程》[清华大学出版社]