- Angel中的损失函数
- 1. Angel中的损失函数
- 2. Angel中Loss的实现
- 3. Loss Function的Json
- 3.1 无参数的损失函数
- 3.2 参数的损失函数
Angel中的损失函数
1. Angel中的损失函数
Angel中有丰富的损失函数, 可分为两类
- 分类损失函数
- 回归损失函数
分类损失函数如下表所示:
| 名称 | 表达式 | 描述 |
|---|---|---|
| CrossEntoryLoss | 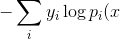 }) }) |
用于分类, 逻辑回归是一种特例, 也可以用于多分类Softmax, 它要求输入是概率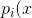 ), 而不是 ), 而不是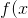 ) ) |
| LogLoss | 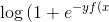 })}) })}) |
用于分类, 是逻辑回归的损失函数, 可以看成是CrossEntoryLoss函数的一种特列, 用Sigmoid的方式具体化了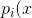 ) ) |
| SoftmaxLoss | 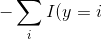 \log\frac{x^{x_i}}{\sum_je^{x_j}}) \log\frac{x^{x_i}}{\sum_je^{x_j}}) |
它是CrossEntoryLoss的特殊形式, 用Softmax的方式具体化了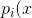 ) ) |
| HingeLoss | 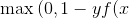 )}) )}) |
SVM的损失函数 |
用图形化表示如下:
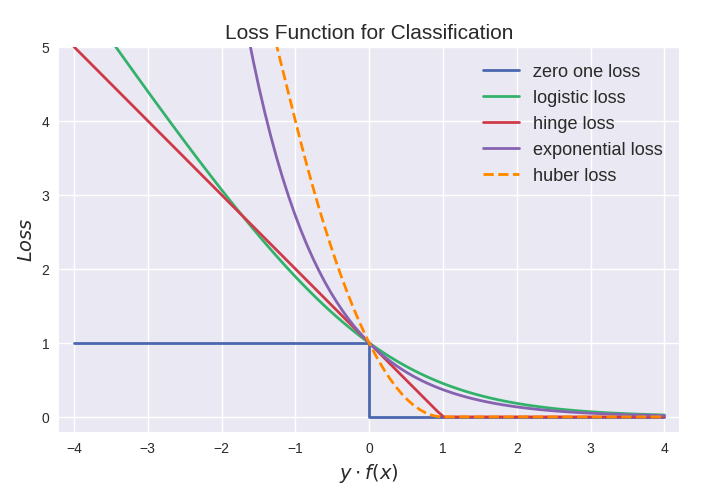
回归损失函数如下表所示
| 名称 | 表达式 | 描述 | ||
|---|---|---|---|---|
| L2Loss | \ | _2^2) | 用于回归, 是最小二乘回归的损失函数 |
| HuberLoss |  -\frac{\delta}{2}),&abs(x)>\delta\\\frac{1}{2}x^2,&abs(x)\le\delta\end{array}\right.) -\frac{\delta}{2}),&abs(x)>\delta\\\frac{1}{2}x^2,&abs(x)\le\delta\end{array}\right.) |
用于回归, 它在0附近用二次函数, 在其它地方用一次函数, 解决了绝对值函数在0附近不可导的问题, 用Huber损失得到的模型较为橹棒 |
用图形化表示如下:
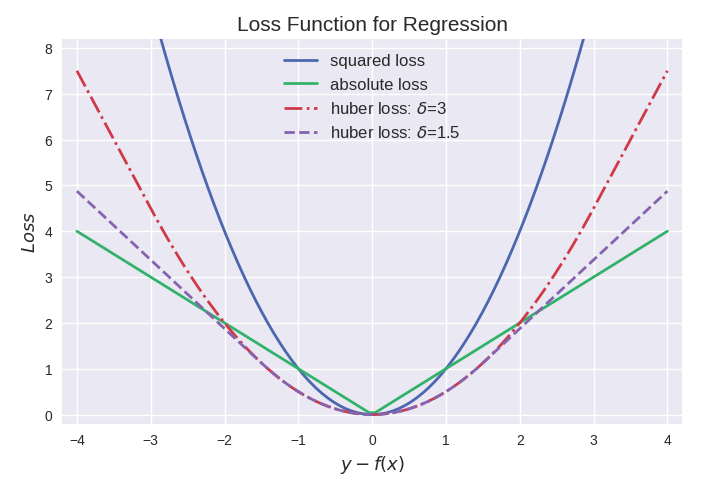
2. Angel中Loss的实现
Angel中的损失函数都实现了LossFunc Trait, 如下:
trait LossFunc extends Serializable {def calLoss(modelOut: Matrix, graph: AngelGraph): Doubledef loss(pred: Double, label: Double): Doubledef calGrad(modelOut: Matrix, graph: AngelGraph): Matrixdef predict(modelOut: Matrix): Matrix}
可见, angel中的loss的不仅有计算loss的功能, 还有计算梯度, 预测两项功能. 正是由于在Loss中实现了梯度计算, 才使反向传导有了起点. 在LossLayer中计算梯度就是直接调用lossFunc的calGrad, 如下:
override def calGradOutput(): Matrix = {val start = System.currentTimeMillis()status match {gradOutput = lossFunc.calGrad(output, graph)status = STATUS.Backwardcase _ =>}val end = System.currentTimeMillis()gradOutput}
另外一项功能是预测, 在LossLayer中计算预测值就是直接调用lossFunc的predict, 如下:
override def predict(): Matrix = {status match {case STATUS.Null =>calOutput()case _ =>}lossFunc.predict(output)}
3. Loss Function的Json
3.1 无参数的损失函数
除了huberloss外, 其它的lossfunc匀为无参数的损失函数, 有两种表达方式, 如下
"lossfunc": "logloss""lossfunc": {"type": "logloss"}
3.2 参数的损失函数
只有huberloss, 具体如下:
"lossfunc": {"type": "huberloss","delta": 0.1}
