- 2.1 误差与过拟合
2.1 误差与过拟合
我们将学习器对样本的实际预测结果与样本的真实值之间的差异成为:误差(error)。定义:
- 在训练集上的误差称为训练误差(training error)或经验误差(empirical error)。
- 在测试集上的误差称为测试误差(test error)。
- 学习器在所有新样本上的误差称为泛化误差(generalization error)。
显然,我们希望得到的是在新样本上表现得很好的学习器,即泛化误差小的学习器。因此,我们应该让学习器尽可能地从训练集中学出普适性的“一般特征”,这样在遇到新样本时才能做出正确的判别。然而,当学习器把训练集学得“太好”的时候,即把一些训练样本的自身特点当做了普遍特征;同时也有学习能力不足的情况,即训练集的基本特征都没有学习出来。我们定义:
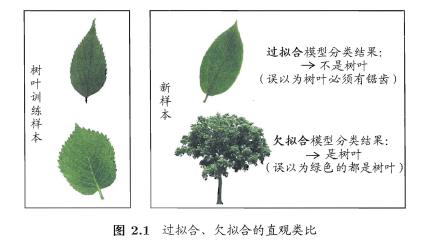
- 学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了,称为:过拟合(overfitting)。
- 学习能太差,训练样本的一般性质尚未学好,称为:欠拟合(underfitting)。
可以得知:在过拟合问题中,训练误差十分小,但测试误差教大;在欠拟合问题中,训练误差和测试误差都比较大。目前,欠拟合问题比较容易克服,例如增加迭代次数等,但过拟合问题还没有十分好的解决方案,过拟合是机器学习面临的关键障碍。