- 5.4 全局最小与局部最小
5.4 全局最小与局部最小
模型学习的过程实质上就是一个寻找最优参数的过程,例如BP算法试图通过最速下降来寻找使得累积经验误差最小的权值与阈值,在谈到最优时,一般会提到局部极小(local minimum)和全局最小(global minimum)。
* 局部极小解:参数空间中的某个点,其邻域点的误差函数值均不小于该点的误差函数值。* 全局最小解:参数空间中的某个点,所有其他点的误差函数值均不小于该点的误差函数值。
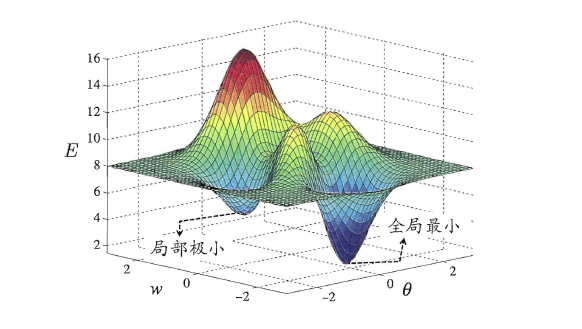
要成为局部极小点,只要满足该点在参数空间中的梯度为零。局部极小可以有多个,而全局最小只有一个。全局最小一定是局部极小,但局部最小却不一定是全局最小。显然在很多机器学习算法中,都试图找到目标函数的全局最小。梯度下降法的主要思想就是沿着负梯度方向去搜索最优解,负梯度方向是函数值下降最快的方向,若迭代到某处的梯度为0,则表示达到一个局部最小,参数更新停止。因此在现实任务中,通常使用以下策略尽可能地去接近全局最小。
* 以多组不同参数值初始化多个神经网络,按标准方法训练,迭代停止后,取其中误差最小的解作为最终参数。* 使用“模拟退火”技术,这里不做具体介绍。* 使用随机梯度下降,即在计算梯度时加入了随机因素,使得在局部最小时,计算的梯度仍可能不为0,从而迭代可以继续进行。
