- 8.2 EM算法数学推导
8.2 EM算法数学推导
在上篇极大似然法中,当样本属性值都已知时,我们很容易通过极大化对数似然,接着对每个参数求偏导计算出参数的值。但当存在隐变量时,就无法直接求解,此时我们通常最大化已观察数据的对数“边际似然”(marginal likelihood)。
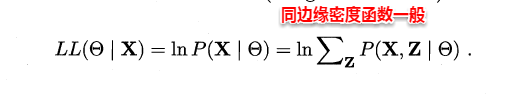
这时候,通过边缘似然将隐变量Z引入进来,对于参数估计,现在与最大似然不同的只是似然函数式中多了一个未知的变量Z,也就是说我们的目标是找到适合的θ和Z让L(θ)最大,这样我们也可以分别对未知的θ和Z求偏导,再令其等于0。
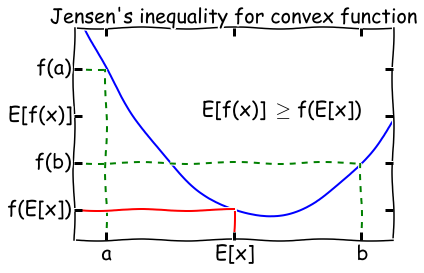
然而观察上式可以发现,和的对数(ln(x1+x2+x3))求导十分复杂,那能否通过变换上式得到一种求导简单的新表达式呢?这时候 Jensen不等式就派上用场了,先回顾一下高等数学凸函数的内容:
Jensen’s inequality:过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方。理解起来也十分简单,对于凸函数f(x)’’>0,即曲线的变化率是越来越大单调递增的,所以函数越到后面增长越厉害,这样在一个区间下,函数的均值就会大一些了。
因为ln(*)函数为凹函数,故可以将上式“和的对数”变为“对数的和”,这样就很容易求导了。
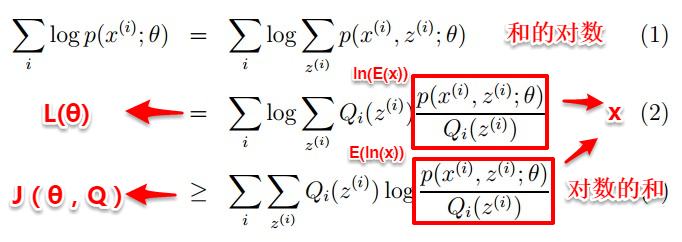
接着求解Qi和θ:首先固定θ(初始值),通过求解Qi使得J(θ,Q)在θ处与L(θ)相等,即求出L(θ)的下界;然后再固定Qi,调整θ,最大化下界J(θ,Q)。不断重复两个步骤直到稳定。通过jensen不等式的性质,Qi的计算公式实际上就是后验概率:
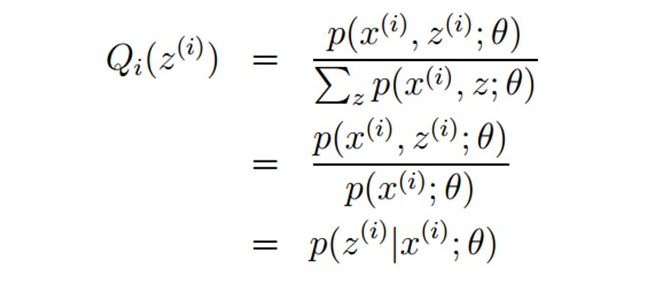
通过数学公式的推导,简单来理解这一过程:固定θ计算Q的过程就是在建立L(θ)的下界,即通过jenson不等式得到的下界(E步);固定Q计算θ则是使得下界极大化(M步),从而不断推高边缘似然L(θ)。从而循序渐进地计算出L(θ)取得极大值时隐变量Z的估计值。
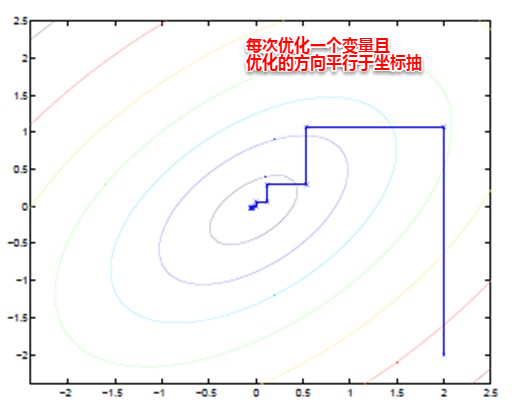
EM算法也可以看作一种“坐标下降法”,首先固定一个值,对另外一个值求极值,不断重复直到收敛。这时候也许大家就有疑问,问什么不直接这两个家伙求偏导用梯度下降呢?这时候就是坐标下降的优势,有些特殊的函数,例如曲线函数z=y^2+x^2+x^2y+xy+…,无法直接求导,这时如果先固定其中的一个变量,再对另一个变量求极值,则变得可行。