• 10.1 距离度量

    10.1 距离度量

    谈及距离度量，最熟悉的莫过于欧式距离了，从年头一直用到年尾的距离计算公式：即对应属性之间相减的平方和再开根号。度量距离还有其它的很多经典方法，通常它们需要满足一些基本性质：

    1.png

    最常用的距离度量方法是“闵可夫斯基距离”（Minkowski distance)：

    2.png

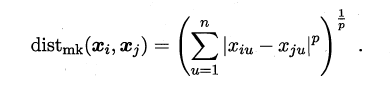
    当p=1时，闵可夫斯基距离即曼哈顿距离（Manhattan distance）：

    3.png

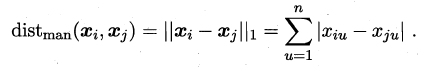
    当p=2时，闵可夫斯基距离即欧氏距离（Euclidean distance）：

    4.png

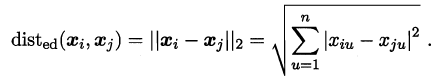
    我们知道属性分为两种：连续属性和离散属性（有限个取值）。对于连续值的属性，一般都可以被学习器所用，有时会根据具体的情形作相应的预处理，例如：归一化等；而对于离散值的属性，需要作下面进一步的处理：

    若属性值之间存在序关系，则可以将其转化为连续值，例如：身高属性“高”“中等”“矮”，可转化为{1, 0.5, 0}。若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“女”，可转化为{（1,0），（0,1）}。

    在进行距离度量时，易知连续属性和存在序关系的离散属性都可以直接参与计算，因为它们都可以反映一种程度，我们称其为“有序属性”；而对于不存在序关系的离散属性，我们称其为：“无序属性”，显然无序属性再使用闵可夫斯基距离就行不通了。

    对于无序属性，我们一般采用VDM进行距离的计算，例如：对于离散属性的两个取值a和b，定义：

    5.png

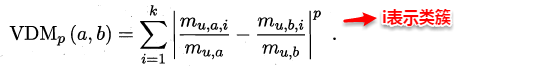
    于是，在计算两个样本之间的距离时，我们可以将闵可夫斯基距离和VDM混合在一起进行计算：

    6.png

    若我们定义的距离计算方法是用来度量相似性，例如下面将要讨论的聚类问题，即距离越小，相似性越大，反之距离越大，相似性越小。这时距离的度量方法并不一定需要满足前面所说的四个基本性质，这样的方法称为：非度量距离（non-metric distance）。