多项式回归

如果你的数据实际上比简单的直线更复杂呢？令人惊讶的是，你依然可以使用线性模型来拟合非线性数据。一个简单的方法是对每个特征进行加权后作为新的特征，然后训练一个线性模型在这个扩展的特征集。这种方法称为多项式回归。

让我们看一个例子。首先，我们根据一个简单的二次方程（并加上一些噪声，如图 4-12）来生成一些非线性数据：

m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)

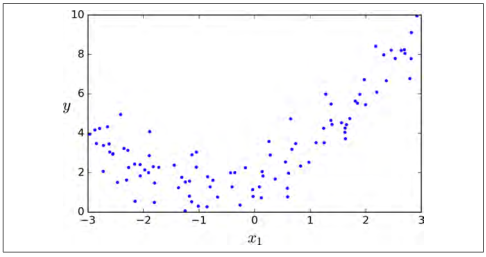
多项式回归 - 图1

图 4-12：生产加入噪声的非线性数据

很清楚的看出，直线不能恰当的拟合这些数据。于是，我们使用 Scikit-Learning 的PolynomialFeatures类进行训练数据集的转换，让训练集中每个特征的平方（2 次多项式）作为新特征（在这种情况下，仅存在一个特征）：

>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2,include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([-0.75275929])
>>> X_poly[0]
array([-0.75275929, 0.56664654])

X_poly现在包含原始特征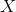并加上了这个特征的平方 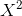X^2 。现在你可以在这个扩展训练集上使用LinearRegression模型进行拟合，如图 4-13：

>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X_poly, y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([ 1.78134581]), array([[ 0.93366893, 0.56456263]]))

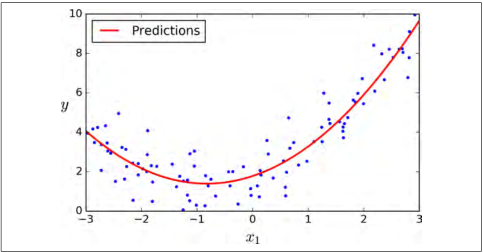
多项式回归 - 图4

图 4-13：多项式回归模型预测

还是不错的，模型预测函数 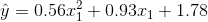$\hat{y}=0.56x_1^2+0.93x_1+1.78$ ，事实上原始函数为 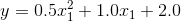y=0.5x_1^2+1.0x_1+2.0 再加上一些高斯噪声。

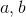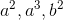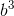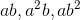请注意，当存在多个特征时，多项式回归能够找出特征之间的关系（这是普通线性回归模型无法做到的）。这是因为LinearRegression会自动添加当前阶数下特征的所有组合。例如，如果有两个特征 a,b ，使用 3 阶（degree=3）的LinearRegression时，不仅有 a^2,a^3,b^2 以及 b^3 ，同时也会有它们的其他组合项 ab,a^2b,ab^2 。

提示

PolynomialFeatures(degree=d)把一个包含个特征的数组转换为一个包含 $\frac{(n+d)!}{d!n!}$ 特征的数组，表示的阶乘，等于 $1 * 2 * 3 \cdots * n$ 。小心大量特征的组合爆炸！