有效的数据表示

您发现以下哪一个数字序列最容易记忆？

• 40, 27, 25, 36, 81, 57, 10, 73, 19, 68
• 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20

乍一看，第一个序列似乎应该更容易，因为它要短得多。 但是，如果仔细观察第二个序列，则可能会注意到它遵循两条简单规则：偶数是前面数的一半，奇数是前面数的三倍加一（这是一个着名的序列，称为雹石序列）。一旦你注意到这种模式，第二个序列比第一个更容易记忆，因为你只需要记住两个规则，第一个数字和序列的长度。 请注意，如果您可以快速轻松地记住非常长的序列，则您不会在意第二个序列中存在的模式。 你只需要了解每一个数字，就是这样。 事实上，很难记住长序列，因此识别模式非常有用，并且希望能够澄清为什么在训练过程中限制自编码器会促使它发现并利用数据中的模式。

记忆，感知和模式匹配之间的关系在 20 世纪 70 年代早期由 William Chase 和 Herbert Simon 着名研究。 他们观察到，专家棋手能够通过观看棋盘5秒钟来记忆所有棋子的位置，这是大多数人认为不可能完成的任务。 然而，只有当这些棋子被放置在现实位置（来自实际比赛）时才是这种情况，而不是随机放置棋子。 国际象棋专家没有比你更好的记忆，他们只是更容易看到国际象棋模式，这要归功于他们对比赛的经验。 注意模式有助于他们有效地存储信息。

就像这个记忆实验中的象棋棋手一样，一个自编码器会查看输入信息，将它们转换为高效的内部表示形式，然后吐出一些（希望）看起来非常接近输入的东西。 自编码器总是由两部分组成：将输入转换为内部表示的编码器（或识别网络），然后是将内部表示转换为输出的解码器（或生成网络）（见图 15-1）。

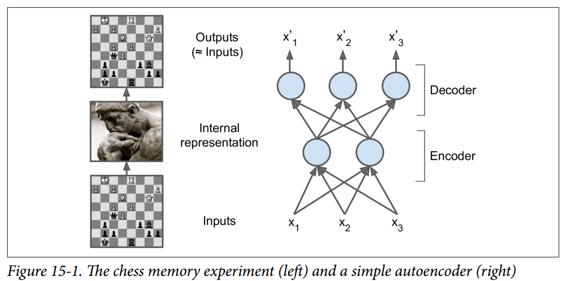
如您所见，自编码器通常具有与多层感知器（MLP，请参阅第 10 章）相同的体系结构，但输出层中的神经元数量必须等于输入数量。 在这个例子中，只有一个由两个神经元（编码器）组成的隐藏层和一个由三个神经元（解码器）组成的输出层。 由于自编码器试图重构输入，所以输出通常被称为重建，并且损失函数包含重建损失，当重建与输入不同时，重建损失会对模型进行惩罚。

由于内部表示具有比输入数据更低的维度（它是 2D 而不是 3D），所以自编码器被认为是不完整的。 不完整的自编码器不能简单地将其输入复制到编码，但它必须找到一种方法来输出其输入的副本。 它被迫学习输入数据中最重要的特征（并删除不重要的特征）。

我们来看看如何实现一个非常简单的不完整的自编码器，以降低维度。