核 PCA(Kernel PCA)
在第 5 章中,我们讨论了核技巧,一种将实例隐式映射到非常高维空间(称为特征空间)的数学技术,让支持向量机可以应用于非线性分类和回归。回想一下,高维特征空间中的线性决策边界对应于原始空间中的复杂非线性决策边界。
事实证明,同样的技巧可以应用于 PCA,从而可以执行复杂的非线性投影来降低维度。这就是所谓的核 PCA(kPCA)。它通常能够很好地保留投影后的簇,有时甚至可以展开分布近似于扭曲流形的数据集。
例如,下面的代码使用 Scikit-Learn 的KernelPCA类来执行带有 RBF 核的 kPCA(有关 RBF 核和其他核的更多详细信息,请参阅第 5 章):
from sklearn.decomposition import KernelPCArbf_pca=KernelPCA(n_components=2,kernel='rbf',gamma=0.04)X_reduced=rbf_pca.fit_transform(X)
图 8-10 展示了使用线性核(等同于简单的使用 PCA 类),RBF 核,sigmoid 核(Logistic)将瑞士卷降到 2 维。
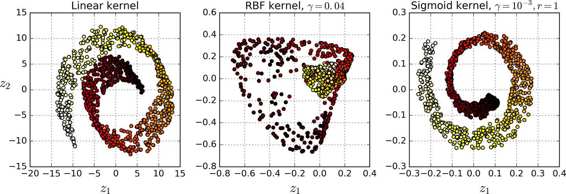
图 8-10 使用不同核的 kPCA 将瑞士卷降到 2 维
选择一种核并调整超参数
由于 kPCA 是无监督学习算法,因此没有明显的性能指标可以帮助您选择最佳的核方法和超参数值。但是,降维通常是监督学习任务(例如分类)的准备步骤,因此您可以简单地使用网格搜索来选择可以让该任务达到最佳表现的核方法和超参数。例如,下面的代码创建了一个两步的流水线,首先使用 kPCA 将维度降至两维,然后应用 Logistic 回归进行分类。然后它使用Grid SearchCV为 kPCA 找到最佳的核和gamma值,以便在最后获得最佳的分类准确性:
from sklearn.model_selection import GridSearchCVfrom sklearn.linear_model import LogisticRegressionfrom sklearn.pipeline import Pipelineclf = Pipeline([("kpca", KernelPCA(n_components=2)),("log_reg", LogisticRegression())])param_grid = [{"kpca__gamma": np.linspace(0.03, 0.05, 10),"kpca__kernel": ["rbf", "sigmoid"]}]grid_search = GridSearchCV(clf, param_grid, cv=3)grid_search.fit(X, y)
你可以通过调用best_params_变量来查看使模型效果最好的核和超参数:
>>> print(grid_search.best_params_){'kpca__gamma': 0.043333333333333335, 'kpca__kernel': 'rbf'}
另一种完全为非监督的方法,是选择产生最低重建误差的核和超参数。但是,重建并不像线性 PCA 那样容易。这里是原因:图 8-11 显示了原始瑞士卷 3D 数据集(左上角),并且使用 RBF 核应用 kPCA 后生成的二维数据集(右上角)。由于核技巧,这在数学上等同于使用特征映射φ将训练集映射到无限维特征空间(右下),然后使用线性 PCA 将变换的训练集投影到 2D。请注意,如果我们可以在缩减空间中对给定实例实现反向线性 PCA 步骤,则重构点将位于特征空间中,而不是位于原始空间中(例如,如图中由x表示的那样)。由于特征空间是无限维的,我们不能找出重建点,因此我们无法计算真实的重建误差。幸运的是,可以在原始空间中找到一个贴近重建点的点。这被称为重建前图像(reconstruction pre-image)。一旦你有这个前图像,你就可以测量其与原始实例的平方距离。然后,您可以选择最小化重建前图像错误的核和超参数。
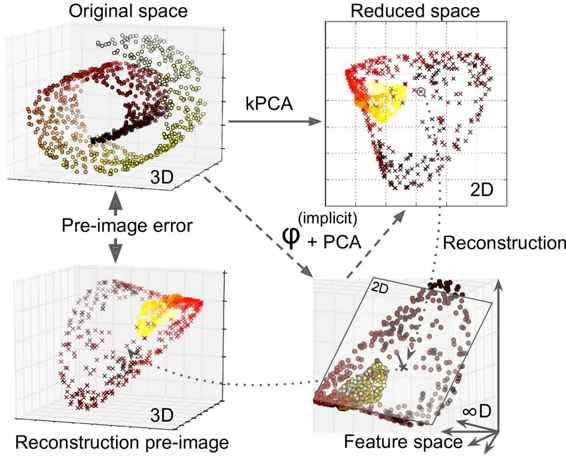
图 8-11 核 PCA 和重建前图像误差
您可能想知道如何进行这种重建。一种解决方案是训练一个监督回归模型,将预计实例作为训练集,并将原始实例作为训练目标。如果您设置了fit_inverse_transform = True,Scikit-Learn 将自动执行此操作,代码如下所示:
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433,fit_inverse_transform=True)X_reduced = rbf_pca.fit_transform(X)X_preimage = rbf_pca.inverse_transform(X_reduced)
概述:默认条件下,
fit_inverse_transform = False并且KernelPCA没有inverse_tranfrom()方法。这种方法仅仅当fit_inverse_transform = True的情况下才会创建。
你可以计算重建前图像误差:
>>> from sklearn.metrics import mean_squared_error>>> mean_squared_error(X, X_preimage) 32.786308795766132
现在你可以使用交叉验证的方格搜索来寻找可以最小化重建前图像误差的核方法和超参数。
LLE
局部线性嵌入(Locally Linear Embedding)是另一种非常有效的非线性降维(NLDR)方法。这是一种流形学习技术,不依赖于像以前算法那样的投影。简而言之,LLE 首先测量每个训练实例与其最近邻(c.n.)之间的线性关系,然后寻找能最好地保留这些局部关系的训练集的低维表示(稍后会详细介绍) 。这使得它特别擅长展开扭曲的流形,尤其是在没有太多噪音的情况下。
例如,以下代码使用 Scikit-Learn 的LocallyLinearEmbedding类来展开瑞士卷。得到的二维数据集如图 8-12 所示。正如您所看到的,瑞士卷被完全展开,实例之间的距离保存得很好。但是,距离不能在较大范围内保留的很好:展开的瑞士卷的左侧被挤压,而右侧的部分被拉长。尽管如此,LLE 在对流形建模方面做得非常好。
from sklearn.manifold import LocallyLinearEmbeddinglle=LocallyLinearEmbedding(n_components=2,n_neighbors=10)X_reduced=lle.fit_transform(X)
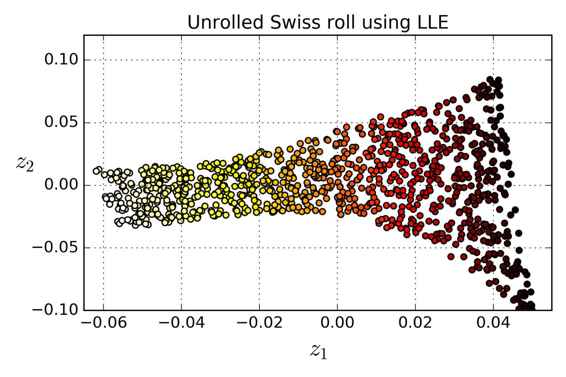
图 8-12 使用 LLE 展开瑞士卷
这是LLE的工作原理:首先,对于每个训练实例 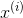 ,该算法识别其最近的
,该算法识别其最近的k个邻居(在前面的代码中k = 10中),然后尝试将 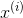 重构为这些邻居的线性函数。更具体地,找到权重
重构为这些邻居的线性函数。更具体地,找到权重 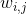 从而使
从而使 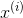 和
和 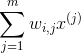 之间的平方距离尽可能的小,假设如果
之间的平方距离尽可能的小,假设如果 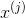 不是
不是 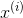 的
的k个最近邻时 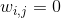 。因此,LLE 的第一步是方程 8-4 中描述的约束优化问题,其中
。因此,LLE 的第一步是方程 8-4 中描述的约束优化问题,其中W是包含所有权重 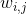 的权重矩阵。第二个约束简单地对每个训练实例
的权重矩阵。第二个约束简单地对每个训练实例 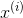 的权重进行归一化。
的权重进行归一化。
公式 8-2 LLE 第一步:对局部关系进行线性建模
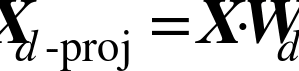
在这步之后,权重矩阵 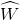 (包含权重
(包含权重 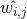 对训练实例的线形关系进行编码。现在第二步是将训练实例投影到一个
对训练实例的线形关系进行编码。现在第二步是将训练实例投影到一个d维空间(d < n)中去,同时尽可能的保留这些局部关系。如果 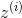 是
是 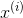 在这个
在这个d维空间的图像,那么我们想要 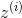 和
和 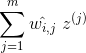 之间的平方距离尽可能的小。这个想法让我们提出了公式8-5中的非限制性优化问题。它看起来与第一步非常相似,但我们要做的不是保持实例固定并找到最佳权重,而是恰相反:保持权重不变,并在低维空间中找到实例图像的最佳位置。请注意,
之间的平方距离尽可能的小。这个想法让我们提出了公式8-5中的非限制性优化问题。它看起来与第一步非常相似,但我们要做的不是保持实例固定并找到最佳权重,而是恰相反:保持权重不变,并在低维空间中找到实例图像的最佳位置。请注意,Z是包含所有 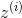 的矩阵。
的矩阵。
公式 8-3 LLE 第二步:保持关系的同时进行降维
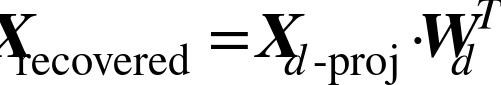
Scikit-Learn 的 LLE 实现具有如下的计算复杂度:查找k个最近邻为O(m log(m) n log(k)),优化权重为O(m n k^3),建立低维表示为O(d m^2)。不幸的是,最后一项m^2使得这个算法在处理大数据集的时候表现较差。
