Adam 优化
Adam,代表自适应矩估计,结合了动量优化和 RMSProp 的思想:就像动量优化一样,它追踪过去梯度的指数衰减平均值,就像 RMSProp 一样,它跟踪过去平方梯度的指数衰减平均值 (见方程式 11-8)。

T 代表迭代次数(从 1 开始)。
如果你只看步骤 1, 2 和 5,你会注意到 Adam 与动量优化和 RMSProp 的相似性。 唯一的区别是第 1 步计算指数衰减的平均值,而不是指数衰减的和,但除了一个常数因子(衰减平均值只是衰减和的1 - β1倍)之外,它们实际上是等效的。 步骤 3 和步骤 4 是一个技术细节:由于m和s初始化为 0,所以在训练开始时它们会偏向0,所以这两步将在训练开始时帮助提高m和s。
动量衰减超参数β1通常初始化为 0.9,而缩放衰减超参数β2通常初始化为 0.999。 如前所述,平滑项ε通常被初始化为一个很小的数,例如 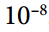 。这些是 TensorFlow 的
。这些是 TensorFlow 的AdamOptimizer类的默认值,所以你可以简单地使用:

实际上,由于 Adam 是一种自适应学习率算法(如 AdaGrad 和 RMSProp),所以对学习率超参数η的调整较少。 您经常可以使用默认值η= 0.001,使 Adam 更容易使用相对于梯度下降。
迄今为止所讨论的所有优化技术都只依赖于一阶偏导数(雅可比矩阵)。 优化文献包含基于二阶偏导数(海森矩阵)的惊人算法。 不幸的是,这些算法很难应用于深度神经网络,因为每个输出有n ^ 2个海森值(其中n是参数的数量),而不是每个输出只有n个雅克比值。 由于 DNN 通常具有数以万计的参数,二阶优化算法通常甚至不适合内存,甚至在他们这样做时,计算海森矩阵也是太慢了。
