反向自动微分
反向自动微分是 TensorFlow 采取的方案。它首先前馈遍历计算图(即,从输入到输出),计算出每个节点的值。然后进行第二次遍历,这次是反向遍历(即,从输出到输入),计算出所有的偏导数。图 D-3 展示了第二次遍历的过程。在第一次遍历过程中,所有节点值已被计算,输入是 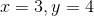 。你可以在每个节点底部右方看到这些值(例如,
。你可以在每个节点底部右方看到这些值(例如,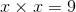 )。节点已被标号,从
)。节点已被标号,从 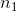 到
到 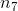 。输出节点是
。输出节点是 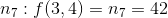 。
。
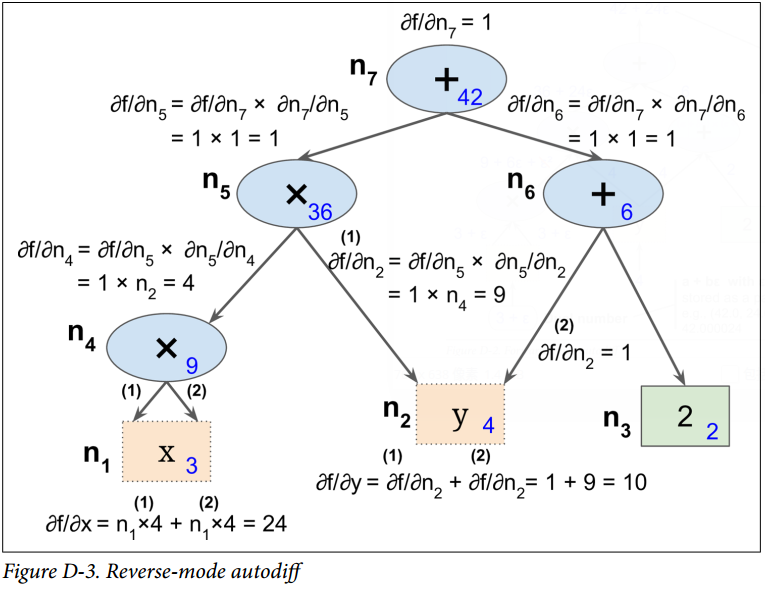
这个计算关于每个连续节点的偏导数的思想逐渐地从上到下遍历图,直到到达变量节点。为实现这个,反向自动微分强烈依赖于链式法则,如公式 D-4 所示。
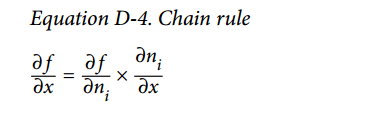
由于 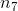 是输出节点,即
是输出节点,即 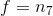 ,所以
,所以 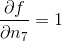 。
。
接着到了图的 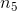 节点:当
节点:当 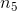 变化时,
变化时,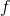 会变化多少?答案是
会变化多少?答案是 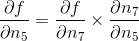 。我们已经知道
。我们已经知道 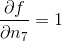 ,因此我们只需要知道
,因此我们只需要知道 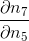 就行。因为
就行。因为 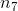 是
是 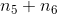 的和,因此可得到
的和,因此可得到 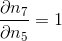 ,因此
,因此 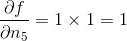 。
。
现在前进到 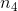 :当
:当 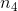 变化时,
变化时,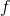 会变化多少?答案是
会变化多少?答案是 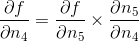 。由于
。由于 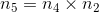 ,我们可得到
,我们可得到 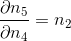 ,所以
,所以 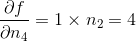 。
。
这个遍历过程一直持续,此时我们达到图的底部。这时我们已经得到了所有偏导数在点 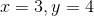 处的值。在这个例子里,我们得到
处的值。在这个例子里,我们得到 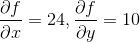 。听起来很美妙!
。听起来很美妙!
反向自动微分是非常强大且准确的技术,尤其是当有很多输入参数和极少输出时,因为它只要求一次前馈传递加上一次反向传递,就可计算所有输出关于所有输入的偏导数。最重要的是,它可以处理任意代码定义的函数。它也可以处理那些不完全可微的函数,只要 你要求他计算的偏导数在该点处是可微的。
如果你在 TensorFlow 中实现了新算子,你想使它与现有的自动微分相兼容,那你需要提供函数,该函数用于构建一个子图,来计算关于新算子输入的偏导数。例如,假设你实现了一个计算其输入的平方的函数,平方算子 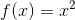 ,在这个例子中你需要提供相应的导函数
,在这个例子中你需要提供相应的导函数 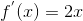 。注意这个导函数不计算一个数值结果,而是用于构建子图,该子图后续将计算偏导结果。这是非常有用的,因为这意味着你可以计算梯度的梯度(为了计算二阶导数,或者甚至更高阶的导数)。
。注意这个导函数不计算一个数值结果,而是用于构建子图,该子图后续将计算偏导结果。这是非常有用的,因为这意味着你可以计算梯度的梯度(为了计算二阶导数,或者甚至更高阶的导数)。
