动量优化

想象一下，一个保龄球在一个光滑的表面上平缓的斜坡上滚动：它会缓慢地开始，但是它会很快地达到最终的速度（如果有一些摩擦或空气阻力的话）。 这是 Boris Polyak 在 1964 年提出的动量优化背后的一个非常简单的想法。相比之下，普通的梯度下降只需要沿着斜坡进行小的有规律的下降步骤，所以需要更多的时间才能到达底部。

回想一下，梯度下降只是通过直接减去损失函数J(θ)相对于权重θ的梯度，乘以学习率η来更新权重θ。 方程是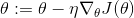：。它不关心早期的梯度是什么。 如果局部梯度很小，则会非常缓慢。

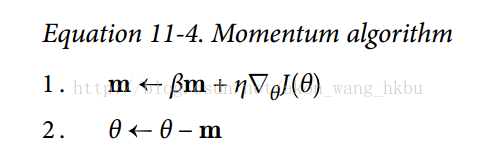
动量优化很关心以前的梯度：在每次迭代时，它将动量矢量m（乘以学习率η）与局部梯度相加，并且通过简单地减去该动量矢量来更新权重（参见公式 11-4）。 换句话说，梯度用作加速度，不用作速度。 为了模拟某种摩擦机制，避免动量过大，该算法引入了一个新的超参数β，简称为动量，它必须设置在 0（高摩擦）和 1（无摩擦）之间。 典型的动量值是 0.9。

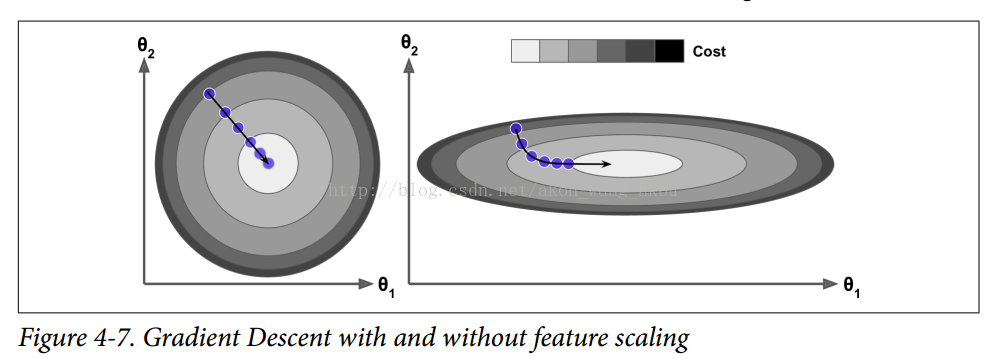
您可以很容易地验证，如果梯度保持不变，则最终速度（即，权重更新的最大大小）等于该梯度乘以学习率η乘以1/(1-β)。 例如，如果β = 0.9，则最终速度等于学习率的梯度乘以 10 倍，因此动量优化比梯度下降快 10 倍！ 这使动量优化比梯度下降快得多。 特别是，我们在第四章中看到，当输入量具有非常不同的尺度时，损失函数看起来像一个细长的碗（见图 4-7）。 梯度下降速度很快，但要花很长的时间才能到达底部。 相反，动量优化会越来越快地滚下山谷底部，直到达到底部（最佳）。

在不使用批标准化的深层神经网络中，较高层往往会得到具有不同的尺度的输入，所以使用动量优化会有很大的帮助。 它也可以帮助滚过局部最优值。

由于动量的原因，优化器可能会超调一些，然后再回来，再次超调，并在稳定在最小值之前多次振荡。 这就是为什么在系统中有一点摩擦的原因之一：它消除了这些振荡，从而加速了收敛。

在 TensorFlow 中实现动量优化是一件简单的事情：只需用MomentumOptimizer替换GradientDescentOptimizer，然后躺下来赚钱！

动量优化的一个缺点是它增加了另一个超参数来调整。 然而，0.9 的动量值通常在实践中运行良好，几乎总是比梯度下降快。