为预测时间序列而训练

现在让我们来看看如何处理时间序列，如股价，气温，脑电波模式等等。 在本节中，我们将训练一个 RNN 来预测生成的时间序列中的下一个值。 每个训练实例是从时间序列中随机选取的 20 个连续值的序列，目标序列与输入序列相同，除了向后移动一个时间步（参见图14-7）。

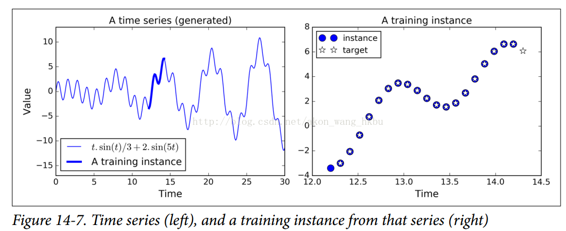
首先，我们来创建一个 RNN。 它将包含 100 个循环神经元，并且我们将在 20 个时间步骤上展开它，因为每个训练实例将是 20 个输入那么长。 每个输入将仅包含一个特征（在该时间的值）。 目标也是 20 个输入的序列，每个输入包含一个值。 代码与之前几乎相同：

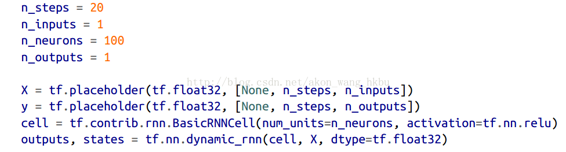
一般来说，你将不只有一个输入功能。 例如，如果你试图预测股票价格，则你可能在每个时间步骤都会有许多其他输入功能，例如竞争股票的价格，分析师的评级或可能帮助系统进行预测的任何其他功能。

在每个时间步，我们现在有一个大小为 100 的输出向量。但是我们实际需要的是每个时间步的单个输出值。 最简单的解决方法是将单元包装在OutputProjectionWrapper中。 单元包装器就像一个普通的单元，代理每个方法调用一个底层单元，但是它也增加了一些功能。Out putProjectionWrapper在每个输出之上添加一个完全连接的线性神经元层（即没有任何激活函数）（但不影响单元状态）。 所有这些完全连接的层共享相同（可训练）的权重和偏差项。 结果 RNN 如图 14-8 所示。

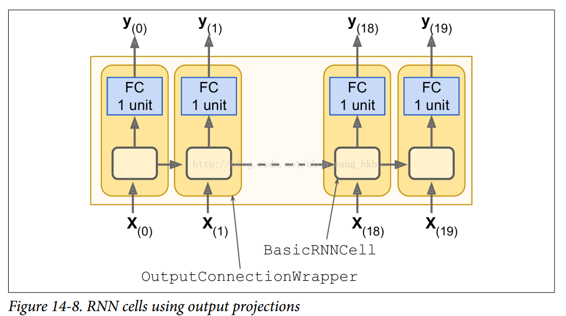
包装单元是相当容易的。 让我们通过将BasicRNNCell包装到OutputProjectionWrapper中来调整前面的代码：

cell =tf.contrib.rnn.OutputProjectionWrapper(
    tf.contrib.rnn.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu),
    output_size=n_outputs)

到现在为止还挺好。 现在我们需要定义损失函数。 我们将使用均方误差（MSE），就像我们在之前的回归任务中所做的那样。 接下来，我们将像往常一样创建一个 Adam 优化器，训练操作和变量初始化操作：

生成 RNN

到现在为止，我们已经训练了一个能够预测未来时刻样本值的模型，正如前文所述，可以用模型来生成新的序列。

为模型提供 长度为n_steps的种子序列, 比如全零序列，然后通过模型预测下一时刻的值；把该预测值添加到种子序列的末尾，用最后面 长度为n_steps的序列做为新的种子序列，做下一次预测，以此类推生成预测序列。

如图 14-11 所示，这个过程产生的序列会跟原始时间序列相似。

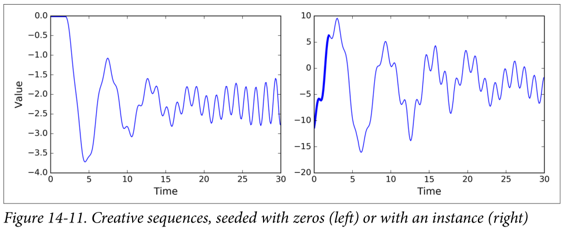
sequence = [0.] * n_steps
for iteration in range(300):
    X_batch = np.array(sequence[-n_steps:].reshape(1, n_steps, 1)
    y_pred = sess.run(outputs, feed_dict={X: X_batch}
    sequence.append(y_pred[0, -1, 0]

如果你试图把约翰·列侬的唱片塞给一个 RNN 模型，看它能不能生成下一张《想象》专辑。

注

约翰·列侬 有一张专辑《Imagine》（1971），这里取其双关的意思

也许你需要一个更强大的 RNN 网络，它有更多的神经元，层数也更多。下面来探究一下深度 RNN。