循环神经元
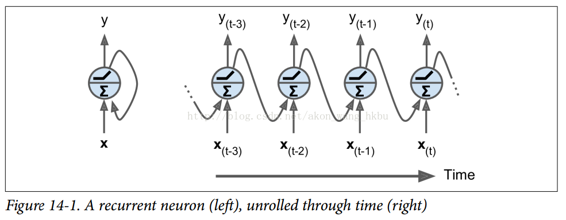
到目前为止,我们主要关注的是前馈神经网络,其中激活仅从输入层到输出层的一个方向流动(附录 E 中的几个网络除外)。 循环神经网络看起来非常像一个前馈神经网络,除了它也有连接指向后方。 让我们看一下最简单的 RNN,它由一个神经元接收输入,产生一个输出,并将输出发送回自己,如图 14-1(左)所示。 在每个时间步t(也称为一个帧),这个循环神经元接收输入 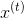 以及它自己的前一时间步长
以及它自己的前一时间步长 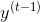 的输出。 我们可以用时间轴来表示这个微小的网络,如图 14-1(右)所示。 这被称为随着时间的推移展开网络。
的输出。 我们可以用时间轴来表示这个微小的网络,如图 14-1(右)所示。 这被称为随着时间的推移展开网络。
你可以轻松创建一个循环神经元层。 在每个时间步t,每个神经元都接收输入向量 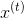 和前一个时间步
和前一个时间步 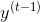 的输出向量,如图 14-2 所示。 请注意,输入和输出都是向量(当只有一个神经元时,输出是一个标量)。
的输出向量,如图 14-2 所示。 请注意,输入和输出都是向量(当只有一个神经元时,输出是一个标量)。
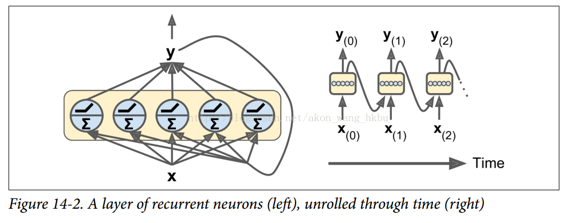
每个循环神经元有两组权重:一组用于输入 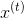 ,另一组用于前一时间步长
,另一组用于前一时间步长 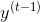 的输出。 我们称这些权重向量为
的输出。 我们称这些权重向量为 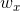 和
和 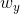 。如公式 14-1 所示(
。如公式 14-1 所示(b是偏差项,φ(·)是激活函数,例如 ReLU),可以计算单个循环神经元的输出。
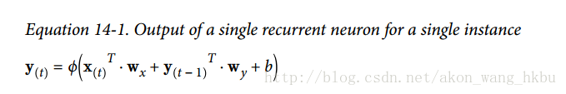
就像前馈神经网络一样,我们可以使用上一个公式的向量化形式,对整个小批量计算整个层的输出(见公式 14-2)。

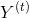 是
是 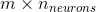 矩阵,包含在最小批次中每个实例在时间步
矩阵,包含在最小批次中每个实例在时间步t处的层输出(m是小批次中的实例数,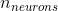 是神经元数)。
是神经元数)。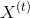 是
是 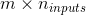 矩阵,包含所有实例的输入的 (
矩阵,包含所有实例的输入的 (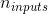 是输入特征的数量)。
是输入特征的数量)。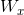 是
是 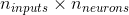 矩阵,包含当前时间步的输入的连接权重的。
矩阵,包含当前时间步的输入的连接权重的。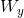 是
是 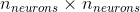 矩阵,包含上一个时间步的输出的连接权重。
矩阵,包含上一个时间步的输出的连接权重。- 权重矩阵
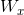 和
和 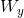 通常连接成单个权重矩阵
通常连接成单个权重矩阵W,形状为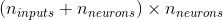 (见公式 14-2 的第二行)
(见公式 14-2 的第二行) b是大小为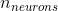 的向量,包含每个神经元的偏置项。
的向量,包含每个神经元的偏置项。
注意,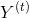 是
是 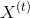 和
和 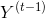 的函数,它是
的函数,它是 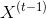 和
和 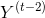 的函数,它是
的函数,它是 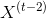 和
和 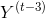 的函数,等等。 这使得
的函数,等等。 这使得 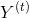 是从时间
是从时间t = 0开始的所有输入(即 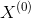 ,
,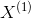 ,…,
,…,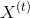 )的函数。 在第一个时间步,
)的函数。 在第一个时间步,t = 0,没有以前的输出,所以它们通常被假定为全零。
